Portrait

Joseph Slote

PhD Candidate, California Institute of Technology

or

I work on quantum and classical complexity theory and related topics in pure mathematics (mostly discrete analysis).


I hold a MSc. in Mathematics and the Foundations of Computer Science from the University of Oxford (2017) and a B.A. in Mathematics from Carleton College (2016). Currently I am a 5th-year CMS PhD student at Caltech, advised by Chris Umans.


Curriculum Vitae

In Preparation

Recent Preprints (arXiv)

Papers

Talks

  • Conference Talk (2023): "Noncommutative Bohnenblust–Hille Inequalities with applications to low-degree learning" at TreilVolberg, University of Würzburg.
  • Workshop Talk (2022): "Fourier Analysis in Quantum Circuit Complexity" at Analysis on the Hypercube with applications to quantum computing, AIM. A similar talk was also given at ICERM and the Probability and Analysis Webinar. (Slides)
  • Conference Paper (2018): "Knot Embeddings in Improper Foldings" with Thomas Bertschinger at the 7th International Meeting on Origami in Science, Mathematics, and Education, held at the University of Oxford. (slides)

Older Research Activity

  • Learning Theory
  • Mathematics of Origami
    • Paper (2018): Knot Embeddings in Improper Foldings with Thomas Bertschinger. Published in Origami7, proceedings of the Seventh International Meeting on Origami in Science, Mathematics, and Education. (highlights, arXiv)
    • Undergraduate Thesis (2016): The Mathematics of Origami with Thomas Bertschinger, O. Claire Spencer, and Sam Vinitsky and supervised by Deanna Haunsperger (full text)

Misc.

  • Psycholinguistics paper (2016): “Conducting spoken word recognition research online: Validation and a new timing method,” published in Behavioral Research Methods (full text)
  • Before coming to Caltech I was the Director of Science and Technology at Dascena, Inc., a Bay Area startup developing ML-based early warning systems for sepsis and other conditions.
full text close

The Expressivity of Artifical Neural Networks (2017)

Masters thesis at the University of Oxford, supervised by Varun Kanade

Deep feedforward artificial neural networks (ANNs) have demonstrated unprecedented learning capabilities in diverse task settings. Possible explanations for their success fall roughly into three categories:

  • Deep networks—relative to wide, shallow networks—may have a superior ability to avoid overfitting;
  • Deep networks create more favorable loss surfaces: training is less likely to settle in bad local minima;
  • Node-for-node, deep networks may support better approximations to functions encountered in practice.

My masters thesis explored the last of these explanations, sometimes called Network Expressivity. Let \(\mathcal{F}_\mathcal{N}\) be the set of functions representable by an ANN \(\mathcal{N}\) as its programmable parameters vary. Because understanding \(\mathcal{F}_\mathcal{N}\) does not depend on the dynamics of a particular training methodology, explorations of expressivity are arguably the most mathematically simple of the above explanations. And yet, the relationship between a network's structure and the space of functions that it can express is far from being satisfactorily characterized, even at the coarse level of depth versus width for fully connected networks.


In my thesis I surveyed known results as well as contributed a few small theorems. Among those surveyed were:

  • Various proofs the universality of depth-two networks as function approximators,
  • Bounds on network structure (depth, width) for approximation of certain function classes,
  • Exponential separations for deep networks—that is, function classes which require exponentially fewer nodes to approximate with deep networks than shallow ones.

My original contributions include:

  • Linear-width universality:
    The set of continuous real-valued functions on \([0,1]^n\) is equal to the \(L_\infty\)-closure of functions implemented by ReLU networks of width \(n+3\).
    This can be seen as the width counterpart to the classic constant-depth universality results. It is a quick corollary to a network narrowing lemma I also proved:
    If a function \(f: \mathbb{R}^n \to \mathbb{R}\) is implemented by an ANN of depth \(d\) and width \(w\), then there exists another network of width \(n+d\) and depth \(\mathcal{O}(dn)\) implementing \(f\) which uses the same set of activation functions along with the identity.
    While it isn't too difficult to transform a wide, shallow network into a deep, narrow one (see the full text for an argument), going the other direction appears very difficult. In fact, I believe this difficulty lies at the heart of understanding function expression by artificial neural networks.
  • A lower bound on the size of a network required to approximate certain Lipschitz functions. Roughly, it says:
    There exist \(K\)-Lipschitz functions \(f: [0,1]^n\to \mathbb{R}\) such that any any network admitting an \(\varepsilon\)-close approximation to \(f\) must have more than \[\frac{2^{n/2}}{\sqrt[3]{2\log(7B/\varepsilon)}}\] nodes.
    This is in analogy to the classical Shannon result that there aren't enough shallow boolean circuits to implement all \(2^{2^n}\) functions from \(\{0,1\}^n\) to \(\{0,1\}\).
  • An exploration into the principle of mutual simulability:

    If two activation functions \(\sigma, \theta\) both exhibit depth-two universality, then any network with \(\sigma\) units may be closely approximated by a network with \(\theta\) units by replacing each \(\sigma\) node with an approximating gadget composed of \(\theta\) nodes.

    Using this principle, I showed that function classes which provide exponential separations for networks composed of one kind of activation function often provide exponential separations for networks composed of another.

close

Error Propagation in the Boson Sampler

Introduced by Aaronson and Arkhipov in 2013, the Boson Sampler is a quantum-computing device which produces samples from a probability distribution associated with the scattering of photons through a lattice of linear optical elements. It is one of the most promising avenues to demonstrating quantum supremacy because the sampling problem it solves is believed to be hard for classical computers.

While the promise BosonSampling holds is thrilling, Aaronson and Arkhipov's result is for an idealized device, one where the input photons are prepared perfectly and the optical lattice perfectly implements the prescribed unitary. For the boson sampler to represent a true refutation of the Strong Church-Turing thesis, its physical realization must be able to closely-approximate the idealized version's operation—that is, it must be robust to realistic errors in state preparation and operation.

Supervised by Ivan Deutsch, I worked with Tyler Keating to characterize how Gaussian noise in photon state preparation propagates to error in the probability distribution from which the device samples. We discovered these errors grow only linearly in the dimension of the space, suggesting the "noisy boson sampling" problem solved by a physical realization of the device could realistically maintain the classical hardness of the idealized device. Techniques used were largely elementary, some borrowed from Bernstein and Vazirani's original paper on quantum complexity theory. Unfortunately, publication of our finding was preempted by the publication of a similar result by V.S. Scheschnovch, albeit with a different mathematical approach.

full text close

Knot Embeddings in Improper Foldings

Published in the proceedings of the 7th International Meeting on Origami in Science, Mathematics, and Education.

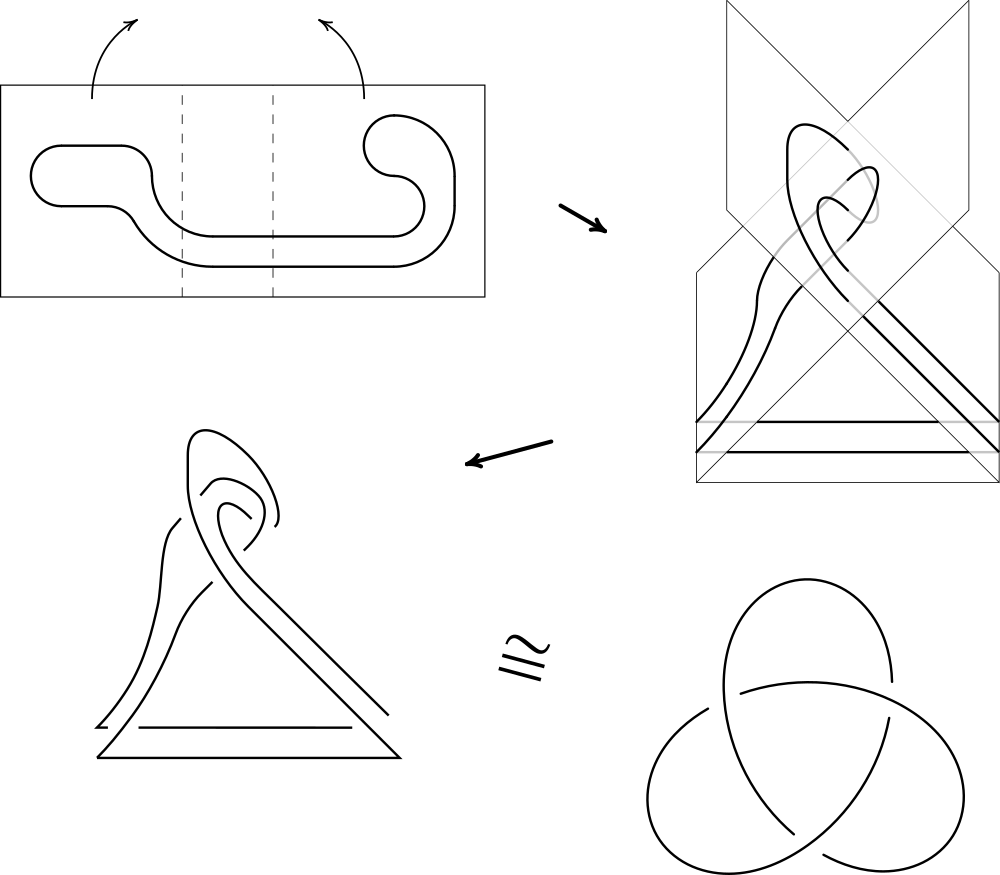
In this improper folding, a closed, simple curve is mapped to the trefoil knot.

This paper represents the first focused study of origami knot theory. In it we introduce a topological model for origami folding, define a novel knot invariant—the fold number—based on origami principles, and resolve a 20-year-old conjecture of Jacques Justin.

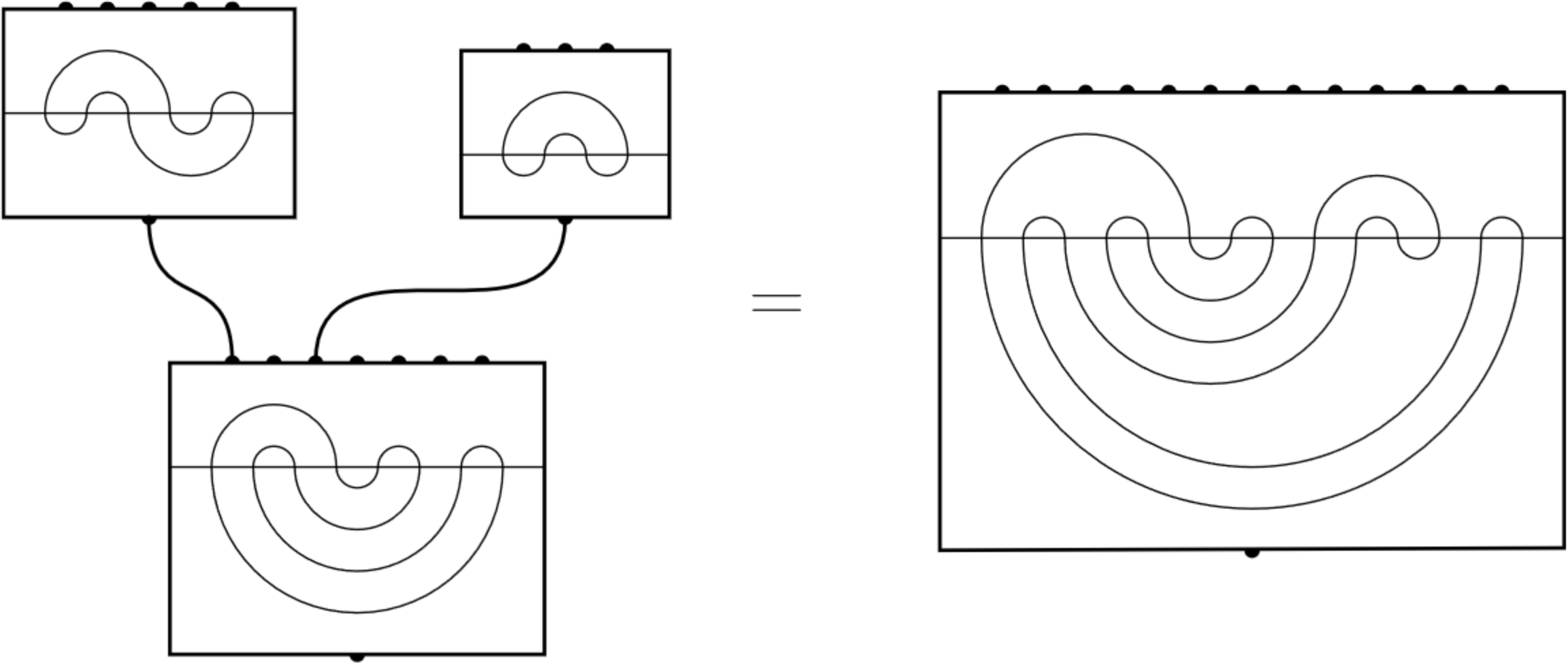
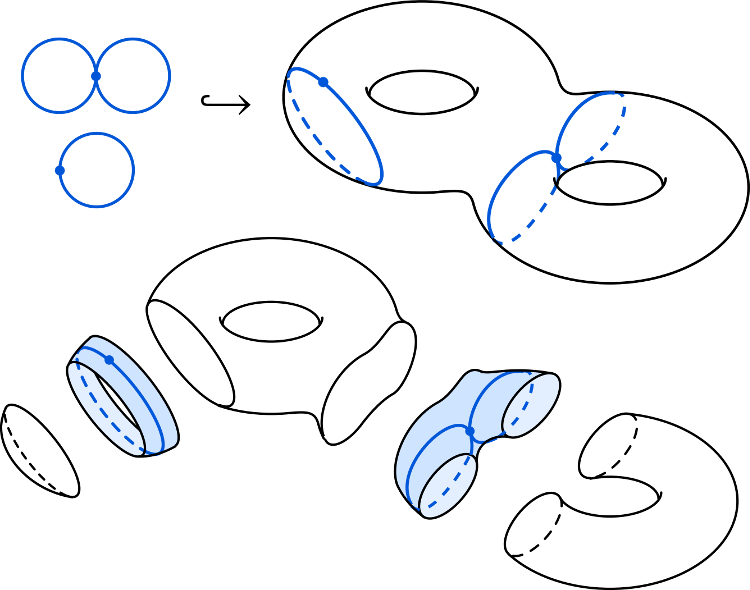
Origami can be formalized as the set of maps from the square to \(\mathbb{R}^3\) which are piecewise-linear (composed of creases) and which preserve the distance between points on the paper (no tearing or stretching). Usually, the mathematical study of these origami maps is restricted to "physically-realizable" maps, which are the closure of the set of injective origami maps. (See Demaine & O'Rourke 2007 for an excellent overview).

However, if one allows an origami folding to nontrivially intersect (such as in the figure above), knots can be formed! We show that knots are present as one-dimensional submaps of non-physically-realizable origami foldings, and indeed for any tame knot \(K\) there exists a folding which admits an equivalent knot as a submap. This motivates the definition of the fold number of a knot \(K\) as the minimum number of folds in an origami folding which admits an equivalent knot to \(K\). We present one loose upper-bound on this invariant, but many question about it remain, including whether or not it is constant.

Further, we address a conjecture made by Jacques Justin in his seminal 1997 work, "Towards a mathematical theory of Origami." He proposed that if an origami folding is physically realizable, its perimeter is mapped to the unknot. We resolve this conjecture positively in the case where the paper is simply-connected.

WIP full text close

Operad Techniques in Meander Enumeration

Meander composition.

Closed meanders of order \(n\) are classes of Jordan curves that transversally intersects the \(x\)-axis \(n\) times, modulo homeomorphisms that map upper to upper and lower to lower half-planes. Meander enumeration (how many meanders are there of order \(n\)?) is a longstanding open problem.

I defined an \(n\)-ary combination operator which creates a larger meander from smaller ones. This operator gives rise to an operad where each meander of size \(n\) corresponds to a morphism from \(1\) to \(n\). Using this structure, one may then derive a recurrence relation by counting how many ways to combine meanders of smaller size modulo certain symmetries.

However, the recurrence is only part of the puzzle as the Meander operad is not finitely generated: for many \(n\) there exist indecomposable meanders which cannot be created by combining smaller ones. These "prime" meanders are particularly serpentine, and fortunately easily characterized: a meander is prime if and only its permutation (the order of its intersections with the \(x\)-axis if you walk along the meander curve) is a simple permutation (that is, a permutation which does not map proper non-singleton intervals to intervals). Given the known difficulty of counting simple permutations, this primality result may suggest that meanders are similarly difficult to enumerate.

close

Surface Separation

A multigraph \(G\) \(k\)-separates a surface \(S\) if there is an embedding \(\phi:G\hookrightarrow S\) such that \(S\backslash\mathrm{Im}(\phi)\) has \(k\) connected components. This separation is minimal if additionally no proper subgraph of \(G\) \(k\)-separates \(S\) under \(\phi\).

The pictured graph \(G\) has an embedding on the 2-torus such it separates the surface into three connected components, while no proper subgraph does so under the same embedding. Therefore \(G\) 3-separates the 2-torus.

Classical questions in topological graph theory (such determining the minimum-genus orientable surface in which a graph \(G\) embeds) are deeply connected to \(k\)-separatingness, and embeddings are also minimal appear in a variety of applied math contexts because they are the boundaries of Voronoi tesselations on surfaces.

In this work we introduce an extension of rotation systems that allows us to give clean descriptions of when graphs \(k\)-separate and minimally \(k\)-separate the orientable surface of genus \(g\). One might also ask about the computational hardness of deciding if a graph \(k\)-separates a surface or minimally \(k\)-separates a surface. We showed both these questions are \(\mathbf{NP}\)-Complete, but the former is fixed-parameter tractable in both \(k\) and \(g\). That is, for constant \(k\) or constant \(g\), we have polytime algorithms.